Distilling JRuby: Frames and Backtraces

Welcome back JRuby fans. I took a poll on twitter about what distilling article to do next, and frames and backtraces was the clear winner - so here we are! (three months later).

In previous “distilling” articles, I discussed how methods are dispatched, and then how the scope of variables in each method and block is managed. The scope and dispatch rules are only part of the big picture, however. Ruby, as a programming language, must gather rich information about the execution of the program, and must be able to share this with the developer when errors occur. Furthermore, Ruby itself provides a number of kernel-level methods for accessing and manipulating the current invocation stack (such as Kernel.caller).

This article is all about how JRuby implements those concepts.

Overview #

A frame in JRuby parlance is a representation of a method call, block call, eval, etc. kept for presentation to the developer. A backtrace is a representation of the active method stack at any point in time - in other words, it’s a stack of frames. In Java, this would typically be referred to as a ‘stack trace’ - at least, that’s the most direct counterpart.

It can be difficult when juggling a language implementation around in your head to realize that the trace we’re talking about is specific to the method calls in Ruby itself. JRuby may execute a number of “native” methods (code written in Java) that do not show up as part of this backtrace - the code that must run in between steps of the Ruby code executing is implementation-specific to JRuby; the Ruby developer shouldn’t care what internal magic JRuby had to do to get a method to invoke (nor would they know what to do with that knowledge if they did have it).

While it may not seem incredibly important initially, JRuby goes to great pains to be as compatible as possible with MRI in terms of what backtraces are generated (This ‘compatibility mode’ incurs a certain cost, and it may be preferable to turn this off to give JRuby an opportunity to bypass this internal bookkeeping if, as a developer, you don’t need a backtrace to match MRI; but we’ll get into those experimental optimizations later). Backtrace information turns out to be quite important, as it is the first set of information a developer typically uses to trace execution issues in their own code; if it isn’t accurate (or at least traversable) it could easily make a small problem a big one.

Tracking Frames #

I would like to mention at this point that it would be in your best interests to read the earlier Distilling JRuby articles, if you haven’t already. Method dispatching, scope, and the JIT compiler are all entertwined with the concept of frames, and I will be talking about these various relationships throughout this article.

You may recall that during the article regarding tracking variable scope, I mentioned that the ThreadContext is consulted on a number of occasions to find data in the variable table. At the time, I was talking about how variables are managed; but that same context class acts as the main source for tracking the frames of method invocation. We saw previously that when a Ruby method is dispatched, a variant of method named preMethod{...}() would be called on the ThreadContext class, and that would in turn tell the ThreadContext to create another DynamicScope object and put it on the top of the stack. It turns out this is exactly where the frame is managed as well. Here is a block of code I showed from the JRuby codebase in that previous article:

public void preMethodFrameAndScope(RubyModule clazz, String name, IRubyObject self, Block block, StaticScope staticScope) {
    RubyModule implementationClass = staticScope.getModule();
    pushCallFrame(clazz, name, self, block); // <-- What we care about this time
    pushScope(DynamicScope.newDynamicScope(staticScope));
    pushRubyClass(implementationClass);
}

Note how this method not only creates a new scope to represent the method’s static scope, but also calls pushCallFrame(...). This is where the new frame is created to represent the method that is being invoked. This frame is represented by a ‘org.jruby.runtime.Frame’ object, which is put on the top of the frame stack.

By most accounts, the Frame object in JRuby is a simple mutable Java bean. The class is relatively simple, and carries a few key pieces of information:

• The object that owns the code being invoked
• The name of the method (or block or eval) being invoked
• The visibility of the method
• The name of the file where the invocation of the frame occurred.
• The line number in the calling file where the invocation of the frame occurred.

… and that’s it! This is basically all that is required to produce a single line in a backtrace. The entire stack of frames then, in turn, represents the entire backtrace.

The Magic Line Number #

While the program is executing, the line number is constantly changing. The frame has some idea of this line number, but only in terms of when the method was called in the enclosing code - it’s not a live representation. However, when you think about a running program, the number on the top of the trace is constantly changing - and on top of that, the frame that is the top of the trace is constantly changing as well - so who is keeping track of this magic number?

It turns out it’s the ThreadContext again, where an integer is kept to keep track of the most current line number (and actually the most current file, as well). In the basic (interpreted) mode of JRuby, the various AST nodes (control statements like if and while, blocks, methods, etc) all have their line number baked into them. When they are invoking, they will update the line number on the thread context. For example, here is the top part of the ‘interpret’ method on org.jruby.ast.IfNode:

@Override
public IRubyObject interpret(Ruby runtime, ThreadContext context, IRubyObject self, Block aBlock) {
    ISourcePosition position = getPosition();
    context.setFile(position.getFile());
    context.setLine(position.getStartLine());
    // ...

For JIT compiler fans, note that it also manages the line number like the interpreted nodes, but as usual is a little more obscure. Two things are done for the JIT compiler: first - code is generated that will call into the ThreadContext to update the line number information like above (See ASTCompiler#compileNewLine). Additionally, however, the line numbers are also actually written into the generated Java bytecode using the standard label/line-number bytecode structures (This will provide distinct advantages in generating backtraces, as we will see later).

As the various code is invoked, this number is constantly being changed to represent the position from the original source. When a new method or block is invoked, that value is copied onto the frame and preserved. This allows the frame to keep track of when it lost control of the execution, while the thread context keeps track of the live line number.

Let’s take a look at a sample backtrace for a specific example:

./another.rb:7:in `do_something_else': undefined method `call' for nil:NilClass (NoMethodError)
from ./another.rb:3:in `do_something'
from test.rb:5:in `run'
from test.rb:9

So what this tells us is that in the method ‘do_something_else’ in another.rb, on line 7, we had a NoMethodError trying to call the method ‘call’ on a nil variable. Additionally, we know the three method calls it took to get to this point. Here is a diagram that shows what the frame stack looks like in the runtime at the moment this occurs (as usual, I’ve done some hand-wavy magic here to simplify a few less-important details…):

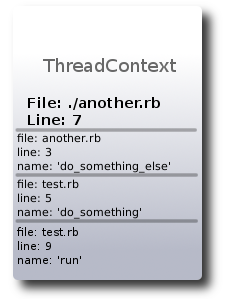
As you can see, the line number stored on the frame correlates to the position in the previous call where the invocation occurred. Also notice that the thread context carries the currently active file and line - but the method name is inferred from the top frame. This mixed relationship, while effective for the way that frames are recorded, can be confusing at first.

Managing Frames at Runtime #

JRuby tries to avoid creating a huge volume of frame objects during execution; in general, the expectation is that a program is going to invoke a lot of methods during execution. If each method was represented by a frame, that would mean a lot of frame objects. To combat this, the frame objects are pre-allocated on the frame stack, and reused. Since programs are generally going to repeatedly traverse up and down the frame-stack, hovering around the same depth of execution, this is one place in Java code where pooling of objects probably makes good sense. Rather than JRuby creating thousands and thousands of frame objects, it will only create enough for the deepest level of execution per thread.

Internally speaking, the ThreadContext class keeps a growable Frame[], but in the process it also ensures that each slot is pre-filled with a ready-to-use frame object. If the allocation needs to grow, the array is increased by a capacity, the existing frame objects are moved to the new array, and the new empty slots are filled with additional Frame allocations.

When a Frame object is set up for use, some variant of the #updateFrame method is called, which basically captures all of the invocation information - it effectively behaves as a constructor:

public void updateFrame(RubyModule klazz, IRubyObject self, String name,
Block block, String fileName, int line, int jumpTarget) {
    this.self = self;
    this.name = name;
    this.klazz = klazz;
    this.fileName = fileName;
    this.line = line;
    this.block = block;
    this.visibility = Visibility.PUBLIC;
    this.isBindingFrame = false;
    this.jumpTarget = jumpTarget;
}

Dispatching Options #

In all of the past three articles, I have brushed by the CallConfiguration enumeration. This enum is a pretty significant lynch-pin in the dispatching and execution of program flow, as it decides a number of things about method and block invocation. Each method may be dispatched using a number of possible call configurations, based on the state of the running program, and the needs of code block being executed. This CallConfiguration decides not only whether a Frame object is required for the call, but also whether or not a Scope is required. This abstraction is very useful as both the interpreter, and the JIT-compiled code dispatch using this configuration strategy.

Just as certain methods may not require an explicit scope (no variables are mutated), some methods also don’t require frames. With both scope and frame, the primary reasons for skipping their use is performance. In the case of scope, the code which manages this is entirely transparent; you don’t care how your variables are managed, as long as they are managed.

However, with frames it’s not that simple. We’ve already discussed how method invocations can be compiled in to Java code in JRuby - effectively avoiding the overhead of making a series of reflection calls in favor for a generated block of Java code that properly preps the Ruby context, and invokes the method through the call site. In this process, a number of possible invocations can be generated - some that setup the frame constructs, and some that don’t. If you tell Ruby it can optimize away as much as possible through flags, it will generate these method connectors to be ultra-super-cool-fast.

Strictly speaking, to turn off frames in the compilation process, you simply need to set ‘jruby.compile.frameless’ to true - although to get the most speed, you could instead set ‘jruby.compile.fastest’ (which implies a number of other settings as well).

It should be noted that, by default, these settings are turned off, and both are marked as experimental. By leaving them disabled by default, it ensures that JRuby, out of the box, is compatible with MRI Ruby as it pertains to generated backtraces and frame manipulation, and is as stable as possible. Turning them on can easily break certain frameworks and libraries that expect the frame or backtrace to be consistent, and manageable. In many cases, however, your application won’t need that kind of control over the frame, and you may not care that the backtrace be exact.

Here are some general rules followed when dispatching to a method or block:

• A full frame will always be used if compatibility mode is enabled (jruby.compile.frameless is set to false).
• Certain system-level invocations (such as the ’eval’ method) get a frame no matter what, as they are frame aware.
• In all other cases either a backtrace-only frame (a “lite” frame) will be used at most.
• If jruby.compile.fastest is set to true, then frames will not be used at all unless it is required by the running program to exist. This obviously has some impact on the readability of the execution.

As mentioned above, readability of backtraces is an issue with jruby.compile.fastest – less accurate information will be available. For example, the trace above that was used looks like this when run with fastest-compilation on:

./another.rb:7:in `do_something_else': undefined method `call' for nil:NilClass (NoMethodError)
from ./another.rb:3:in `do_something'
from :1:in `run'
from :1

Note that all frames but the top are completely unaware of the execution details - in many cases this may be sufficient information to fix a problem, but it is certainly less than what is available in compatibility mode.

The ’lite’ backtrace-only frame I mentioned is basically a trimmed down representation that doesn’t hold on to references to the owning object. While this can reduce the usability of the frame (particularly for methods like ’eval’ that may need to interact with the caller), it’s a significant optimization as it takes several objects off the object graph, preventing long-lived references to live objects in from the program flow (such as the object that is being invoked against). This will allow the GC to handle these objects sooner than may otherwise be possible.

Execution Flow #

When an error occurs, the execution needs to stop and unwind from the exception to the first point it is properly handled (with a rescue, or all the way out of the program). This can make following the JRuby code complicated, as Java exception flow is used as the back-bone for the Ruby exception flow, and so the two intermingle and must be kept separate in your mind.

The primary class that represents an exception in Ruby is org.jruby.RubyException, which is the JRuby native implementation of the Exception class in Ruby. There are a number of subclasses that are constructed (such as ArgumentError, as we will see below) that let Ruby code handle errors in a typed way, but effectively everything extends this ‘Exception’ class. Now, while this is called ‘Exception’, it’s not actually a Java exception. It extends RubyObject (like all JRuby native peers), and is a representation of a Ruby exception for the runtime, but has no effect on Java as anything but a standard object.

However, RubyExceptions can be encountered during execution, and that should interrupt execution. Somehow this has to be handled in Java code. As an example, the ’to_sym’ method on RubyString is implemented natively in Java, and that method, by contract, should throw an exception if the string is empty.

    $ ruby -e '"".to_sym'
    -e:1:in 'to_sym': interning empty string (ArgumentError)
    from -e:1
    $ jruby -e '"".to_sym'
    -e:1: interning empty string (ArgumentError)

As it turns out, the easiest way to interrupt Java code like this is to use a Java exception. For this, JRuby uses the class org.jruby.RaiseException, which is, in fact, a real Java exception. As the name hints, it represents the execution of a ‘raise’ keyword in Ruby (which is roughly analogous to a Java throw, but is actually a method on the Thread class). RaiseException contains the RubyException representing the error in Ruby code.

When Ruby code invokes ‘raise’, this method will delegate through org.jruby.RubyKernel#raise, which for the most part will end up throwing a new RaiseException. Now, this is where it gets tricky to distinguish the two. Keep in mind that the RaiseException simply exists so JRuby can back up the Java code to find the right Ruby code to handle the error. On the other side of the equation, the code in JRuby follows a pattern roughly like this:

public void interpret() {
    try {
        runBodyRubyCode(...);
    }
    catch(RaiseException e) {
        runRescueRubyCode(e.getRubyException());
    }
    finally {
        runEnsureRubyCode(...);
    }
}

This is pseudo-code mixed from the AST RescueNode and EnsureNode, but it captures the idea. First, the code is run - then, if a RaiseException occurs, the exception is sent into a rescue block of code. Keep in mind that when the rescue code is run, the Ruby exception is unboxed so it’s directly accessible to that code block (as it always is in Ruby). The ensure code is actually handled by a separate AST node (since it may be included independently of rescue), but the concept is the same as seen above.

The JIT obviously changes how this code is actually invoked (via generated Java code), but the same general logic applies.

If an exception isn’t handled via a mechanism like raise, then the RaiseException itself is handled by the Java bootstrap (such as the executable). This has some special consequences when it comes to embedded code, and we’ll get into that shortly.

Additionally, there is a special version of RaiseException called NativeException (this also exists in MRI) - this is a special wrapper for exceptions that occur in Java code called from JRuby code. When this happens, the stack trace for those native parts is actually preserved in the Ruby stack up to the point the Ruby code invoked the Java code. Here is an example of a backtrace that was created by an exception occurring in some Java code:

java/lang/NumberFormatException.java:48:in 'forInputString': java.lang.NumberFormatException: For input string: "15123sdfs" (NativeException)
from java/lang/Long.java:419:in 'parseLong'
from java/lang/Long.java:468:in 'parseLong'
from ./another.rb:7:in 'do_something_else'
from ./another.rb:5:in 'do_something'
from [script]:5:in 'run'
from [script]:9

Constructing Backtraces #

Throughout this article, we’ve seen examples of backtraces that were (seemingly) generated off of the frame stack. To create a proper backtrace, the currently active frame stack must be copied and turned into a point-in-time snapshot of backtrace information. When an error occurs, the backtrace is captured with participation between the RaiseException, RubyException, and the ThreadContext.

When the RubyException is constructed, it asks the ThreadContext to create a backtrace, which then iterates over the current frame stack, creating a RubyStackTraceElement array. This array is then bound to the RubyException. Here is a sample of the loop that creates the backtrace array (I’ve trimmed some unnecessary details):

public static IRubyObject createBacktraceFromFrames(Ruby runtime, RubyStackTraceElement[] backtraceFrames) {
    RubyArray backtrace = runtime.newArray();
    if (backtraceFrames == null || backtraceFrames.length <= 0) return backtrace;
    int traceSize = backtraceFrames.length;
    for (int i = 0; i < traceSize - 1; i++) {
        RubyStackTraceElement frame = backtraceFrames[i];
        addBackTraceElement(runtime, backtrace, frame, backtraceFrames[i + 1]);
    }
    return backtrace;
}

In the normal “framed backtrace” workflow, that’s all there is to it. That array can then be used to emit to the console, or whatever else needs to occur.

Interestingly, there are a number of other “super secret” ways the backtrace can be generated. As best as I can tell, these are entirely undocumented on the JRuby site - these are simply custom values for “jruby.backtrace.style” - these include:

• “raw” - This version provides a very explicit output of what happened, including all of the internal JRuby stack - very useful for JRuby development:

  from java/lang/Long.java:419:in `parseLong'
  from java/lang/Long.java:468:in `parseLong'
  from Thread.java:1460:in `getStackTrace'
  from RubyException.java:143:in `setBacktraceFrames'
  from RaiseException.java:177:in `setException'
  from RaiseException.java:119:in `<init>'
      from RaiseException.java:101:in `createNativeRaiseException'
      from JavaSupport.java:188:in `createRaiseException'
      from JavaSupport.java:184:in `handleNativeException'
      from JavaCallable.java:170:in `handleInvocationTargetEx'
      (... removed the rest for brevity ...)
  

* "raw_filtered" - Just like 'raw', but it omits any Java classes starting with 'org.jruby'. This is handy if you have code-flows that go from Ruby -> Java -> Ruby -> Java, etc - and need to see the Java code intermixed. I've used this when coding in Swing and SWT where event hooks may go into Java, and back into Ruby.
* "ruby_framed" (the default) - This uses the internal Ruby frame stack to generate an MRI-friendly backtrace. "rubinus" is currently compatible with this version. Depending on the settings you have enabled, this can return different values (as described above).
* "ruby_compiled" - This uses the Java stack trace, and parses the compiled class names. When JRuby generates compiled invokers for methods, they will have mangled names that can be re-parsed (looking for sentinels like $RUBY$). Additionally, remember earlier how I said that the line numbers were actually compiled in to the Java code straight from the Ruby code? Well, that means the Java stack trace will automatically have the correct line numbers in it, so building the Ruby backtrace is truly just a matter of parsing the Java StackTraceElement\[\]. Because of the nature of the bytecode and the Java VM capturing this information, when running with jruby.compile.fastest set to true, this mode can actually return <em>more</em> accurate information than ruby_framed will. Note that if a method isn't compiled, it will not show up in the Java stack, and as such the stack will only contain Java methods that were invoked (of which there may be none).
* "ruby_hybrid" (currently disabled) - This version is meant to be able to munge compiled and interpreted information together into a mega-stack-trace, allowing for compiled and interpreted methods to show up in the same stack trace, using the Java stack to (auspiciously) improve performance where possible -- I'm assuming it's commented out due to some flaw in the implementation.

## Embedding JRuby Programs in Java

When embedding JRuby in Java programs, errors that occur can potentially leave the Ruby runtime altogether. When this happens, Java code is in total control. To make this transition as seamless as possible, JRuby performs some nifty tricks with traditional Java stack-traces.

Our old friend RaiseException actually generates the object-graph for a backtrace like above, and then creates a pseudo-Ruby stack in the Java code that lets a Java programmer see where in the Ruby code the error occurred. Here is the example from way up above as generated in Java code:

```bash
Exception in thread "main" javax.script.ScriptException: org.jruby.exceptions.RaiseException: undefined method 'call' for nil:NilClass
 at org.jruby.embed.jsr223.JRubyEngine.wrapException(JRubyEngine.java:112)
 at org.jruby.embed.jsr223.JRubyEngine.eval(JRubyEngine.java:173)
 at realjenius.SampleProgram.main(SampleProgram.java:13)
Caused by: org.jruby.exceptions.RaiseException: undefined method 'call' for nil:NilClass
 at Kernel.call(./another.rb:7)
 at Another.do_something_else(./another.rb:3)
 at Another.do_something([script]:5)
 at MyClass.run([script]:9)
 at (unknown).(unknown)(:1)

Other conversions for the backtrace (such as the fancy NativeException stuff) works naturally with this code as well, allowing for diversions in Ruby code to show up naturally in the Java stack.

Frame Peeking with Ruby Programs #

I previously mentioned Kernel#caller, which is a method for peeking at the going-ons in the Ruby trace. Now that we understand the structure of the frames, it is probably pretty easy to see how they will be used. The implementation of org.jruby.RubyKernel#caller simply calls ThreadContext#createCallerBacktrace which is much like all of the other code we looked at, but it creates a RubyArray containing strings representing the state of the frames in the context at that time.

public IRubyObject createCallerBacktrace(Ruby runtime, int level) {
    int traceSize = frameIndex - level + 1;
    RubyArray backtrace = runtime.newArray(traceSize);

    for (int i = traceSize - 1; i > 0; i--) {
        addBackTraceElement(runtime, backtrace, frameStack[i], frameStack[i - 1]);
    }

    return backtrace;
}

It’s probably also clear by now why optimizations like ‘jruby.compile.fastest’ can break these methods; the frames aren’t there for the ThreadContext to report against.

Conclusion #

While the frame concepts in JRuby in and of themselves aren’t that complicated, you have to have a strong foundational knowledge of how Ruby works and how method dispatching in JRuby works to understand the code flows. I hope I’ve been able to condense the concepts into an easy enough walkthrough.

I’m by no means done with these JRuby articles – I took a little hiatus for work and personal reasons, but hope to have more coming out of the gates real soon. Here is a peek at some possible subjects:

• The Library Load Service
• Continuations (Kernel#callcc)
• Java Proxying and Support
• The New Kid on the Block: Duby

As usual, votes are welcome: Contact Me.

Stay Tuned!